Batter Statistics for 2018 Major League Baseball (MLB) Season
Source:R/data-mlb_players_18.R
mlb_players_18.RdBatter statistics for 2018 Major League Baseball season.
Format
A data frame with 1270 observations on the following 19 variables.
- name
Player name
- team
Team abbreviation
- position
Position abbreviation:
1B= first base,2B= second base,3B= third base,C= catcher,CF= center field (outfield),DH= designated hitter,LF= left field (outfield),P= pitcher,RF= right field (outfield),SS= shortstop.- games
Number of games played.
- AB
At bats.
- R
Runs.
- H
Hits.
- doubles
Doubles.
- triples
Triples.
- HR
Home runs.
- RBI
Runs batted in.
- walks
Walks.
- strike_outs
Strike outs.
- stolen_bases
Stolen bases.
- caught_stealing_base
Number of times caught stealing a base.
- AVG
Batting average.
- OBP
On-base percentage.
- SLG
Slugging percentage.
- OPS
On-base percentage plus slugging percentage.
Examples
d <- subset(mlb_players_18, !position %in% c("P", "DH") & AB >= 100)
dim(d)
#> [1] 429 19
# _____ Per Position, No Further Grouping _____ #
plot(d$OBP ~ as.factor(d$position))
model <- lm(OBP ~ as.factor(position), d)
summary(model)
#>
#> Call:
#> lm(formula = OBP ~ as.factor(position), data = d)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.162185 -0.024185 -0.000745 0.026063 0.149038
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.328490 0.005544 59.252 < 0.0000000000000002 ***
#> as.factor(position)2B -0.013562 0.007663 -1.770 0.077506 .
#> as.factor(position)3B -0.010745 0.007696 -1.396 0.163433
#> as.factor(position)C -0.026553 0.007432 -3.573 0.000394 ***
#> as.factor(position)CF -0.017528 0.007766 -2.257 0.024520 *
#> as.factor(position)LF -0.004264 0.007766 -0.549 0.583277
#> as.factor(position)RF -0.004305 0.007731 -0.557 0.577911
#> as.factor(position)SS -0.016769 0.008197 -2.046 0.041397 *
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.03959 on 421 degrees of freedom
#> Multiple R-squared: 0.04361, Adjusted R-squared: 0.0277
#> F-statistic: 2.742 on 7 and 421 DF, p-value: 0.008569
#>
anova(model)
#> Analysis of Variance Table
#>
#> Response: OBP
#> Df Sum Sq Mean Sq F value Pr(>F)
#> as.factor(position) 7 0.03009 0.0042983 2.7421 0.008569 **
#> Residuals 421 0.65992 0.0015675
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# _____ Simplified Analysis, Fewer Positions _____ #
pos <- list(
c("LF", "CF", "RF"),
c("1B", "2B", "3B", "SS"),
"C"
)
POS <- c("OF", "IF", "C")
table(d$position)
#>
#> 1B 2B 3B C CF LF RF SS
#> 51 56 55 64 53 53 54 43
# _____ On-Base Percentage Across Positions _____ #
out <- c()
gp <- c()
for (i in 1:length(pos)) {
these <- which(d$position %in% pos[[i]])
out <- c(out, d$OBP[these])
gp <- c(gp, rep(POS[i], length(these)))
}
plot(out ~ as.factor(gp))
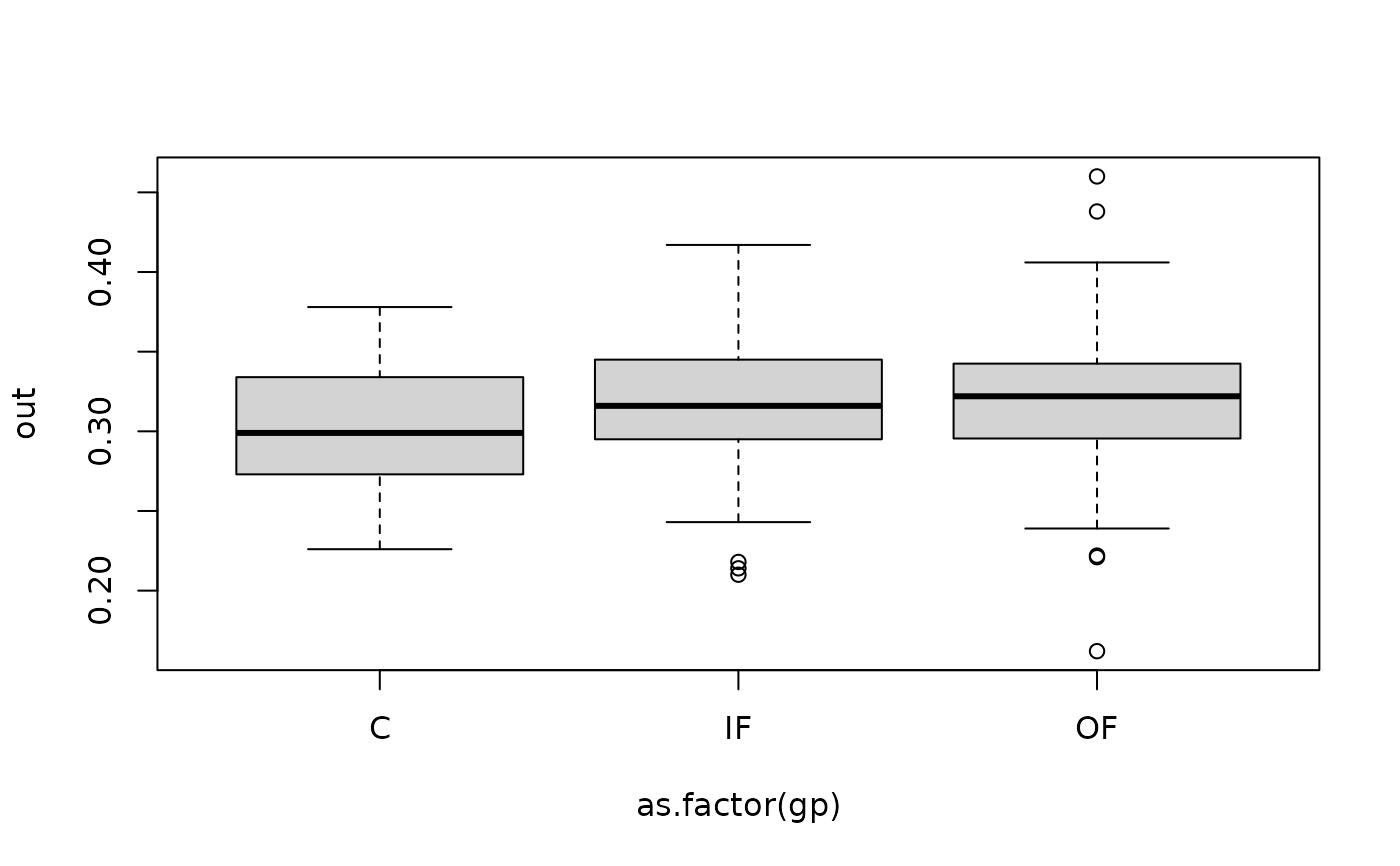summary(lm(out ~ as.factor(gp)))
#>
#> Call:
#> lm(formula = out ~ as.factor(gp))
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.157819 -0.024819 -0.001385 0.027062 0.140181
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.301937 0.004972 60.729 < 0.0000000000000002 ***
#> as.factor(gp)IF 0.016448 0.005695 2.888 0.00408 **
#> as.factor(gp)OF 0.017881 0.005883 3.040 0.00252 **
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.03977 on 426 degrees of freedom
#> Multiple R-squared: 0.02328, Adjusted R-squared: 0.01869
#> F-statistic: 5.077 on 2 and 426 DF, p-value: 0.006624
#>
anova(lm(out ~ as.factor(gp)))
#> Analysis of Variance Table
#>
#> Response: out
#> Df Sum Sq Mean Sq F value Pr(>F)
#> as.factor(gp) 2 0.01606 0.0080314 5.0766 0.006624 **
#> Residuals 426 0.67395 0.0015820
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1